4 Toepassingen in groep verwerken
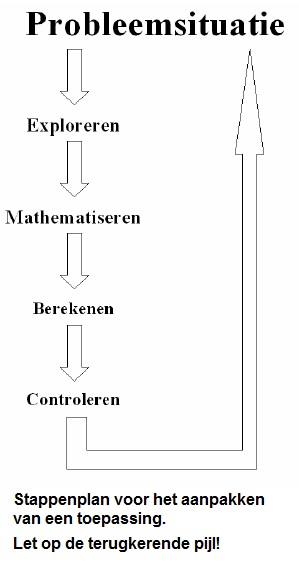Heel wat problemen uit de maatschappelijke leefwereld kunnen aangepakt worden met wiskunde. Het oplossen van zo'n problemen valt onder de noemer toepassingen. Het proces waarbij men met wiskunde naar oplossingen zoekt, valt grofweg uiteen in de vier stappen beschreven in Practicum 2.
Het verschil tussen het oplossen van een probleem zoals in Practica 2 en 3 en een toepassing zit hem in de zoekstrategieën (Stap 2). Bij toepassingen komt het er meestal op neer om in de opgave een wiskundig begrip te herkennen, zoals bijvoorbeeld een rechthoekige driehoek, een functie, een matrix, etc. Het oplossen van het oorspronkelijk probleem vertaalt zich dan in het uitvoeren van bewerkingen met die begrippen. Men verwijst naar deze zoekstrategie als mathematiseren of modelleren. Het oplossen van een toepassing is dus een veredelde vorm van probleemoplossend denken uit Practica 1 en 2. Samengevat komen we bij het aanpakken van een toepassing uit op volgende stappen.
- Stap 1. Het probleem begrijpen Heel vaak kun je het probleem beter begrijpen door het op een andere manier te verwoorden.
- Stap 2. Mathematiseren Herkennen van een wiskundig begrip, en inzien dat het gevraagde kan vertaald worden naar een model: een bewerking, een vergelijking, een stelsel vergelijkingen, een extremumvraagstuk, een matrixvermenigvuldiging, een rechthoekige of een willekeurige driehoek, etc.
- Stap 3. Berekenen Als het wiskundig model opgebouwd is, probeer je dit via rekentechnieken op te lossen.
- Stap 4. Uitkomst interpreteren en controleren Interpretatie van het resultaat, waarbij je rekening houdt met de context van het probleem. In dit practicum vormen de leerlingen groepen van drie tot vier. Ze verwerken samen toepassingen op matrices, waarbij gevraagd wordt om hier en daar iets aan te vullen. Zo laten ze zien dat ze de nieuwe technieken beheersen. De leerkracht speelt een ondersteunende rol voor minder sterke leerlingen. Na het aanvullen vergelijken de leerlingen hun antwoorden met de verbetering. Tenslotte oefenen ze de technieken uit deze toepassingen in met nieuwe opdrachten.
- Practicumbundel (inleiding, opdracht en evaluatieformulier)
- Toepassingen op matrices - Opgave
- Oefeningen - Opgave
- G. Delaleeuw, Mathematiseren en oplossen van problemen voor de derde graad tso/kso, Cahiers T³ Europe Vlaanderen nr.9 (2006).
