A passion for math and math education

Vijfde jaar 6u

• Update! Cover met een inleiding, wat er van de leerling wordt verwacht en afspraken. In deze map bewaren de leerlingen hun portfoliobundels. Ze wordt dan ook best afgedrukt op verhard papier.

   -1. Nieuw! Portfolio Deel O Hoofdstuk 1 (Veeltermen: Basisbegrippen)

   -2. Nieuw! Portfolio Deel O Hoofdstuk 2 (Veeltermen: Deling van veelterm door veelterm)

   -3. Nieuw! Portfolio Deel O Hoofdstuk 3 (Veeltermen: Deling van veelterm door x-a)

   -4. Nieuw! Portfolio Deel O Hoofdstuk 4 (Veeltermen: Toepassingen)

1. Portfolio Deel I Hoofdstuk 1 (Precalculus 1: Herhaling)
2. Portfolio Deel I Hoofdstuk 2 (Precalculus 1: Veeltermfuncties)
3. Portfolio Deel I Hoofdstuk 3 (1) (Precalculus 1: Rationale functies)
4. Portfolio Deel I Hoofdstuk 3 (2) (Precalculus 1: Rationale functies)
5. Portfolio Deel I Hoofdstuk 4 (Precalculus 1: Irrationale functies)
6. Portfolio Deel I Interludium (1) (Precalculus 1: Machten en machtswortels, bewerkingen met functies, inverse functies, soorten functies)
7. Portfolio Deel I Interludium (2) (Precalculus 1: Machten en machtswortels, bewerkingen met functies, inverse functies, soorten functies)
8. Portfolio Deel I Hoofdstuk 5 (1) (Precalculus 1: Exponentiële functies)
9. Portfolio Deel I Hoofdstuk 5 (2) (Precalculus 1: Exponentiële functies)
10. Portfolio Deel I Hoofdstuk 6 (1) (Precalculus 1: Logaritmische functies)
11. Portfolio Deel I Hoofdstuk 6 (2) (Precalculus 1: Logaritmische functies)
12. Portfolio Deel I Hoofdstuk 7 (Precalculus 1: Exponentiële en logaritmische vergelijkingen en ongelijkheden)
13. Portfolio Deel II Hoofdstuk 1 (Goniometrie: Basisbegrippen)
14. Portfolio Deel II Hoofdstuk 2 (1) (Goniometrie: Formules van de goniometrie)
15. Portfolio Deel II Hoofdstuk 2 (2) (Goniometrie: Formules van de goniometrie)
16. Portfolio Deel II Hoofdstuk 3 (Goniometrie: Goniometrische vergelijkingen en ongelijkheden)
17. Portfolio Deel II Hoofdstuk 4 (1) (Precalculus 2: Goniometrische functies)
18. Portfolio Deel II Hoofdstuk 4 (2) (Precalculus 2: Goniometrische functies)
19. Portfolio Deel II Hoofdstuk 5 (Precalculus 2: Cyclometrische functies)
20. Portfolio Deel III Hoofdstuk 1 (1) (Matrices: Matrices)
21. Portfolio Deel III Hoofdstuk 1 (2) (Matrices: Matrices)
22. Portfolio Deel III Hoofdstuk 2 (1) (Matrices: Lineaire stelsels)
23. Portfolio Deel III Hoofdstuk 2 (2) (Matrices: Lineaire stelsels)
24. Portfolio Deel III Hoofdstuk 3 (1) (Matrices: Determinanten)
25. Portfolio Deel III Hoofdstuk 3 (2) (Matrices: Determinanten)
26. Portfolio Deel IV Hoofdstuk 1 (1) (Complexe getallen: Cartesische vorm)
27. Portfolio Deel IV Hoofdstuk 1 (2) (Complexe getallen: Cartesische vorm)
28. Portfolio Deel IV Hoofdstuk 2 (1) (Complexe getallen: Polaire vorm en Euler-vorm)
29. Portfolio Deel IV Hoofdstuk 2 (2) (Complexe getallen: Polaire vorm en Euler-vorm)
30. Portfolio Deel V Hoofdstuk 1 (1) (Logica: Uitsprakenlogica)
31. Portfolio Deel V Hoofdstuk 1 (2) (Logica: Uitsprakenlogica)
32. Portfolio Deel V Hoofdstuk 2 (Logica: Predicatenlogica)
33. Portfolio Deel VI Hoofdstuk 1 (1) (Rijen: Basisbegrippen)
34. Portfolio Deel VI Hoofdstuk 1 (2) (Rijen: Basisbegrippen)
35. Portfolio Deel VI Hoofdstuk 2 (1) (Rijen: Limiet van een rij)
36. Portfolio Deel VI Hoofdstuk 2 (2) (Rijen: Limiet van een rij)
37. Portfolio Deel VI Hoofdstuk 3 (Rijen: Discrete veranderingsprocessen)
38. Portfolio Deel VII Hoofdstuk 1 (1) (Limieten)
39. Portfolio Deel VII Hoofdstuk 1 (2) (Limieten)
40. Portfolio Deel VII Hoofdstuk 1 (3) (Limieten)
41. Portfolio Deel VII Hoofdstuk 2 (Asymptoten)
42. Portfolio Deel VII Hoofdstuk 3 (1) (Continuïteit)
43. Portfolio Deel VII Hoofdstuk 3 (2) (Continuïteit)

Vijfde jaar +2u

• Cover met een inleiding, wat er van de leerling wordt verwacht en afspraken. In deze map bewaren de leerlingen hun portfoliobundels. Ze wordt dan ook best afgedrukt op verhard papier.

1. Portfolio Deel XV Hoofdstuk 1 (1) (Vectorvlak en euclidisch vlak: Het vectorvlak V_2)
2. Portfolio Deel XV Hoofdstuk 1 (2) (Vectorvlak en euclidisch vlak: Het vectorvlak V_2)
3. Portfolio Deel XV Hoofdstuk 2 (Vectorvlak en euclidisch vlak: Het Euclidisch vlak E_2)
4. Portfolio Deel XVI Hoofdstuk 1 (Getaltheorie: Inleidende begrippen en definities)
5. Portfolio Deel XVI Hoofdstuk 2 (Getaltheorie: Deelbaarheid van gehele getallen)
6. Portfolio Deel XVI Hoofdstuk 3 (Getaltheorie: Priemgetallen)
7. Portfolio Deel XVI Hoofdstuk 4 (1) (Getaltheorie: Grootste gemene delers en kleinste gemene veelvouden)
8. Portfolio Deel XVI Hoofdstuk 4 (2) (Getaltheorie: Grootste gemene delers en kleinste gemene veelvouden)
9. Portfolio Deel XVII Hoofdstuk 1 (Vectorruimten: Voorkennis in inleidende begrippen)
10. Portfolio Deel XVII Hoofdstuk 2 (Vectorruimten: Vectorruimten)
11. Portfolio Deel XVII Hoofdstuk 3 (Vectorruimten: Deelruimten)
12. Portfolio Deel XVII Hoofdstuk 4 (Vectorruimten: Basis)
13. Portfolio Deel XVII Hoofdstuk 5 (Vectorruimten: Dimensie)

Zesde jaar 6u

• Cover met een inleiding, wat er van de leerling wordt verwacht en afspraken. In deze map bewaren de leerlingen hun portfoliobundels. Ze wordt dan ook best afgedrukt op verhard papier.

1. Portfolio Deel VIII Hoofdstuk 1 (Afgeleiden: Het begrip afgeleide)
2. Portfolio Deel VIII Hoofdstuk 2 (Afgeleiden: Veeltermfuncties)
3. Portfolio Deel VIII Hoofdstuk 3 (Afgeleiden: Rationale en irrationale functies)
4. Portfolio Deel VIII Interludium 1 (Afgeleiden: limieten-asymptoten-hoekpunt,keerpunt,verticale raaklijn)
5. Portfolio Deel VIII Hoofdstuk 4 (Afgeleiden: Exponentiële en logaritmische functies)
6. Portfolio Deel VIII Interludium 2 (Afgeleiden: Regel van de l'Hospital)
7. Portfolio Deel VIII Hoofdstuk 5 (Afgeleiden: Goniometrische en cyclometrische functies)
8. Portfolio Deel IX Hoofdstukken 1 en 2 (Telproblemen: Inleiding en motivatie, groeperingen zonder herhaling)
10. Portfolio Deel IX Hoofdstuk 3 (Telproblemen: Groeperingen met herhaling, herhalingsoefeningen)
11. Portfolio Deel X Hoofdstuk 1 (Kansrekenen 1: Gebeurtenissen en kansen)
12. Portfolio Deel X Hoofdstukken 2 en 3 (Kansrekenen 1: Voorwaardelijke kans en onafhankelijkheid, wet van totale kans en wet van Bayes)
14. Portfolio Deel XI Hoofdstuk 1 (1) (Integralen: Bepaalde integralen)
15. Portfolio Deel XI Hoofdstuk 1 (2) (Integralen: Bepaalde integralen)
16. Portfolio Deel XI Hoofdstuk 2 (Integralen: Toepassingen op bepaalde integralen)
17. Portfolio Deel XI Hoofdstuk 3 (1) (Integralen: Onbepaalde integralen en integratietechnieken)
18. Portfolio Deel XI Hoofdstuk 3 (2) (Integralen: Onbepaalde integralen en integratietechnieken)
19. Portfolio Deel XII Hoofdstuk 1 (Ruimtemeetkunde: Vectoren en coördinaten in de ruimte)
20. Portfolio Deel XII Hoofdstuk 2 (Ruimtemeetkunde: Rechten)
21. Portfolio Deel XII Hoofdstuk 3 (Ruimtemeetkunde: Vlakken)
22. Portfolio Deel XII Hoofdstuk 4 (Ruimtemeetkunde: Bijzondere rechten en vlakken, afstanden)
23. Portfolio Deel XIII Hoofdstuk 1 (1) (Beschrijvende statistiek: Gegevens verzamelen en beschrijven, beschrijvende maten)
24. Portfolio Deel XIII Hoofdstuk 1 (2) (Beschrijvende statistiek: Gegevens verzamelen en beschrijven, beschrijvende maten)
25. Portfolio Deel XIII Hoofdstuk 2 (Beschrijvende statistiek: De normale verdeling)
26. Portfolio Deel XIV Hoofdstuk 1 (Kansrekenen 2 en verklarende statistiek: Stochasten)
27. Portfolio Deel XIV Hoofdstuk 2 (Kansrekenen 2 en verklarende statistiek: Bijzondere kansverdelingen)

---

Voor de leerling

Het is een misvatting te denken dat het vermogen om problemen op te lossen louter aangeboren is. Doelgericht veelvuldig trainen en reflecteren kan een aanzienlijk voordeel opleveren. Maar het oefenen in probleemoplossend denken hoort ons inziens te voldoen aan een aantal randvoorwaarden.

• Het is onverstandig om problemen altijd zonder context te zien. Niet alleen kan het oplossen van vragen binnen een bepaalde context of referentiekader meer motiverend werken, men kan op die manier ook nieuwe leerstof inoefenen.
• Elke leerling hoort op eigen tempo en op een aangepast niveau problemen te kunnen oplossen. Meer specifiek opteren we voor zelfgereguleerde differentiatie. Er wordt een minimumdoel voor de klas als geheel gesteld, en elke leerling kan op zijn of haar niveau een eigen oefentraject uitstippelen.
• De leerling moet in staat zijn aan zelfevaluatie te doen door zijn/haar oplossingen naast een modeloplossing te leggen.
• Tot slot dient de leerling te reflecteren over de eigen ontwikkeling: welke competenties en leerstofonderdelen beheers ik goed, en hoe kan ik de zwakke punten verbeteren? Op die manier speelt de leerling de hoofdrol bij het `managen' van het leerproces.
• De leerkracht of docent moet kunnen beoordelen of je die probleemoplossende vaardigheden in voldoende mate ontwikkelt. Er volgt dus een evaluatie van het proces, waarbij je ook feedback krijgt.

We hebben ervoor gekozen om zo'n project te realiseren aan de hand van een zogenaamd portfolio, een persoonlijke map waarin de leerling beschrijft wat hij/kan kan, waaruit dat blijkt en hoe de competenties verder kunnen ontwikkelen worden. Globaal gezien dient een portfolio twee doelen:

• leerlingen kunnen laten zien wat ze geleerd hebben en wat ze in hun mars hebben, en
• het helpt leerlingen te reflecteren over wat ze bereikt hebben en welke (leerstof)onderdelen nog extra oefening vergen.

Wat wordt er van de leerling verwacht?

Elk hoofdstuk uit de cursus is voorzien van oefeningen, die onder verdeeld worden in drie categorieën: basis, verdieping en uitbreiding. Een overzicht van de oefeningen volgens categorie ziet er bijvoorbeeld als volgt uit (zie Deel Precalculus 1 Hoofdstuk 2):

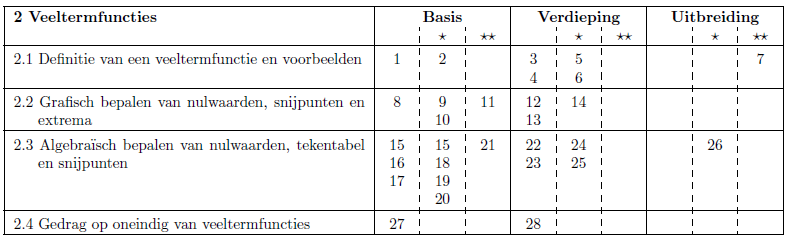
De interpretatie van deze categorieën is als volgt.

• Basis Deze oefeningen zijn bedoeld om de theorie te verwerken, en de basistechnieken die de leerling gezien heeft in de modelvoorbeelden in te oefenen. Alle leerlingen horen dit niveau te halen. Afhankelijk van de afspraken van de leerkracht kan op een toets of proefwerk een afgesproken percentage van de oefeningen bestaan uit basis-en verdiepingsoefeningen. Bijvoorbeeld voor leerlingen met zes wekelijkse lestijden 85% basisoefeningen en 15% verdiepingsoefeningen, voor leerlingen met acht wekenlijkse lestijden 70% basisoefeningen en 30% verdiepingsoefeningen
• Verdieping Deze categorie veronderstelt een grotere beheersingsgraad. Het zijn oefeningen die niet rechtstreeks met de in de les geziene technieken van onder andere modeloefeningen kunnen opgelost worden. Verdiepingsoefeningen vergen extra creativiteit, en laten leerlingen toe door te groeien in probleemoplossend denken. Leerlingen die een wetenschappelijke studierichting in het hoger of universitair onderwijs nastreven horen zich ook te richten naar deze categorie.
• Uitbreiding Bij uitbreidingsoefeningen gaat het om een extra leerinhoud, die niet noodzakelijk is voor het vervolg van de cursus, maar die meer diepgang of hogere vaardigheden vragen. Dit is dus niet een nog hoger niveau dan de verdieping. Bij deze oefeningen worden meestal nieuwe begrippen gedefinieerd. Leerlingen die studies zoals burgerlijk ingenieur of burgerlijk ingenieur-architect ambiëren horen zich ook naar dit niveau te richten.

Verder is elke categorie voorzien van een niveau: 0, 1 of 2 sterren. Al is een verschil in niveau bij basisoefeningen anders te interpreteren dan een verschil in punten bij uitbreidings- en verdiepingsoefeningen. Zo vergt een basisoefening met 0 sterren minder werk dan een basisoefening met 2 sterren (maar daarom is het niet eenvoudiger), en een verdiepingsoefening met 0 sterren eenvoudiger dan een verdiepingsoefening met 2 sterren (daarom vergt het niet minder werk). Het is de bedoeling dat de leerling zelf kiest op welk niveau hij/zij oefeningen maakt. Dat kan best door te starten met een basisoefening met bijvoorbeeld 0 sterren. Als dit moeizaam gaat oefent de leerling verder op dit niveau. Kun de leerling de oefening goed oplossen, dan kan de volgende oefening al een basisoefening met 1 fof 2 sterren zijn, en later overgaan naar verdieping en/of uitbreiding. Zo stelt de leerling zelf een persoonlijk, op maat gemaakt oefentraject samen.

Sommige vragen uit de voorgaande edities van de Vlaamse Wiskunde Olympiade werden opgenomen, alsook vragen uit de vroegere toelatingsexamens van burgerlijk ingenieur, burgerlijk ingenieur-architect, (tand)arts, Koninklijke Militaire School en Burgerluchtvaartschool. Het is de bedoeling om deze oefeningen op te lossen zonder gebruik te maken van de grafische rekenmachine, of enig ander computerrekenpakket (zoals Sage of Maple).

Leerlingen kunnen hun oefeningen controleren door de antwoorden te vergelijken met de antwoorden in de cursus. Die bevinden zich op het einde van elk deel. Maar ook al heeft een leerling het correcte eindantwoord, het is ten sterkste aangewezen dat de leerlingen hun oplossing naast een modeloplossing leggen. De leerkracht kan zo'n modeloplossingen vooraan in de klas leggen, waar leerlingen zelfstandig of met de leerkracht hun oefeningen verbeteren.

Afspraken

1. Tijdens de les wordt er tijd voorzien om aan oefeningen te werken. Daarnaast wordt er verwacht dat leerlingen ook buiten de les regelmatig oefeningen maken.
2. Oefeningen worden gemaakt op cursusbladen. Gemaakte oefeningen waarmee de leerling zijn/haar competentie wil aantonen, wordt in de portfoliobundel gevoegd.
3. Tussentijds verbeteren met een rode pen doet de leerling zelf aan de hand van modeloplossingen die in de klas liggen. Op het einde van elk hoofdstuk kunnen die oplossingen op een digitaal leerplatform zoals Smartschool komen.
4. Na het verbeteren kleurt de leerling in de overzichtstabel (zoals hierboven) zelf het vakje met het nummer van de oefening:
   • groenals de oefening goed en volledig zelfstandig werd opgelost (minstens 70%),
   • oranjeals de oefening matig en/of met wat hulp werd opgelost (tussen 50% en 70%),
   • roodals je de oefeningonvoldoende en/of met veel hulpwerd opgelost (minder dan 50%).
   Na het doorlopen van het oefentraject kan een gedeelte van de overzichtstabel er bijvoorbeeld als volgt uit zien:
   

   Zo weet de leerling bij het voorbereiden van een toets of proefwerk meteen welke oefeningen hij/zij moet hernemen, en bij welke paragraaf er nog wat extra moet geoefend worden.

5. Bij sommige hoofdstukken wordt ook gevraagd om te reflecteren aan de hand van een reflectieformulier.
6. Tijdens de lessen op het relevante deel van de leerstof heeft de leerling de portfoliobundel steeds bij. Er kan steeds worden nagekeken of de leerling tijdens de voorbije les(sen) zinvol oefeningen gemaakt heeft, of je de oefeningen verbeterd zijn en of je de reflectie werd ingevuld.
7. De leerling dient het portfolio in op de dag dat een toets afgelegd wordt over die leerstof. Is je resultaat op de toets nipt of onvoldoende, dan kijkt de leerkracht via het portfolio na of de leerling wel voldoende oefeningen gemaakt hebt, en of je die oefeningen ook verbeterd hebt. Zo niet, dan wordt de leerling aangemaand om in het vervolg meer oefeningen te maken, en/of je oefeningen ook nauwgezet te verbeteren. Is je portfolio wel behoorlijk, dan kan de leerling uitgenodigd worden op een gesprek met de leerkracht, om te reflecteren over studiemethode.

Het portfolio hoeft dus niet op puntentussentijdse evaluatie (TTE) te staan. Wel

• is het de verantwoordelijkheid van de leerling hoeveel oefeningen hij/zij maakt, en op welk niveau (ken jezelf!);
• is de bundel een bewijsstuk van hoe zelfstandig de leerling te werk gaat, en toont de hiermee aan of hij/zij al dan niet een juiste studiehouding heeft;
• dient het portfolio als procesevaluatie, hetgeen in de schoolagenda of een attituderapport kan worden genoteerd.

---

Voor de leerkracht

Portfolio wiskunde is een werkvorm dat, als onderdeel van de cursus Wiskunde In zicht, bestemd is voor leerlingen van de derde graad algemeen secundair onderwijs in de studierichtingen met zes of acht wekelijkse lestijden wiskunde. De noodzaak tot deze werkvorm is gegroeid vanuit de tendens dat klassen met component wiskunde in de derde graad ASO steeds meer heterogeen worden, maar ook om een antwoord te bieden op de negatieve tendens dat leerkrachten bij een nakend C-attest in juni worden gevraagd naar hun aangeboden remediëring naar de leerlingen toe.

Ontstaan. Portfolio wiskunde is sedert 01/09/2010 in opbouw, ten behoeve van de leerlingen van de derde graad van het Onze-Lieve-Vrouwecollege Assebroek te Brugge. Deze werkvorm heeft zeker niet de pretentie origineel te zijn, foutloos te zijn, `af' te zijn of erger nog de intentie te hebben van: `zo moet het'. De auteur wil enkel laten zien: `misschien kan het zo ook'. De werkvorm heeft geleid tot het geven van gelijknamige voordrachten en werkwinkels. Een recente presentatie vindt u hier. Toekomstige data en locaties van zo'n nascholing vindt u op de homepage onder de rubriek Onderwijs, didactische voordrachten, item 9.

Rechten. Portfolio wiskunde is een didactische publicatie, gelicenseerd onder een Creative Commons Naamsvermelding-NietCommercieel-GelijkDelen 3.0 Unported (CC BY-NC-SA). Elke gebruiker wordt geacht op de hoogte te zijn van deze licentievoorwaarden, en ze te aanvaarden. De volledige licentie hiervan is te vinden op de website http://creativecommons.org/licenses/by-nc-sa/3.0/legalcode, een vereenvoudigde (human-readable) versie hiervan op http://creativecommons.org/licenses/by-nc-sa/3.0/deed.nl.

Veelgestelde vragen

• Hoe kan deze werkvorm in het schooljaar gepland worden? Ter informatie geven we enkele schoolagenda's van vorige schooljaren.
  • Agenda vijfde jaar 6 lestijden wiskunde schooljaar 2022-2023
  • Agenda vijfde jaar 6+2 lestijden wiskunde schooljaar 2022-2023
  • Agenda vijfde jaar 8 lestijden wiskunde schooljaar 2014-2015
  • Agenda klas zesde jaar 6 lestijden wiskunde schooljaar 2018-2019
  • Agenda klas zesde jaar 6 lestijden wiskunde schooljaar 2014-2015
• De bestanden worden aangeboden in PDF-formaat. Kan ik een Word-document krijgen? Dat kan niet, want de cursus wordt niet opgemaakt met Word. De auteur hanteert het tekstzetsysteem LaTeX.
• Kan ik de broncode van een portfolio krijgen? Bij wijze van voorbeeld de broncode van de cover en Portfolio 5. We geven ook de links naar de figuren uit dit portfolio, eveneens gemaakt met LaTeX in pstricks: figuur 1, figuur 2, figuur 3 en figuur 4.
• Is elke oefening origineel? Uiteraard niet. Soms is een oefening gedeeltelijk of volledig gebaseerd op, ontleend aan, geïnspireerd op of overgenomen uit één of meerdere (hand)boeken of andere publicaties. Een actuele referentielijst kunt u verkrijgen op de website Wiskunde In zicht.
• Nieuw! Kan ik de uitgewerkte oplossingen krijgen? Je sommige uitgewerkte oefeningen al vrij downloaden op de deelpagina Wiskunde In zicht. Die bestanden worden aangeboden in PDF-formaat (zonder watermerk) en zijn meestal een scan van handgeschreven oplossingen. De andere uitgewerkte oefeningen volgen tijdens de maand juli 2023. Op die webpagina worden ook de bijbehorende cursusdelen van Wiskunde In zicht aangeboden, zowel de blanco versies als de ingevulde versies.
• Hoeveel verdient de auteur hieraan? Het Royalty percentage bedraagt 0%. Dat betekent dat de auteur geen geld verdient aan het online publiceren via issuu.com en ontvangen van bestellingen via lulu.com. De auteur zal dit werk ook in de toekomst gratis houden, zodat de werkvorm Portfolio ook in de toekomst vrij toegankelijk en gratis zal blijven.
• Waar kan ik terecht met andere vragen of opmerkingen? Dat kan eenvoudig door een e-mail te sturen naar koendenaeghel@hotmail.com.

---

U bent bezoeker